Positions planétaires
Le calcul des positions planétaires
Ou comment faire ses propres éphémérides
Les lois de Kepler et de Newton
Historiquement, ce sont les lois de Kepler qui ont été "découvertes" en premier, et pratiquement, ce sont celles ci que nous allons utiliser, un petit peu "traficottées" pour calculer l'orbite des planètes et ainsi leur position...
On a déjà vu les techniques qui avaient permis à Kepler de trouver la position relative des planètes, ceci lui a donné ses lois :
- L'orbite des planètes est une ellipse dont le soleil est l'un des foyers.
- L'aire balayée par le rayon vecteur ( droite joignant le soleil à la planète) en un temps donné est une constante.
- Si on note T le temps pour une planète d'effectuer une orbite et a les demi grand axe de l'ellipse alors t²/a^3=constante.
D'accord, comme ça, c'est pas très clair. Mais cela a permis à Newton de trouver ses lois :
F=ma. Principe des actions réciproques... F(gravitationelle)= -gMm/r².
Ces lois étant plus générales, on va les utiliser pour retrouver les lois de Kepler. Ceci nous permettra de découvrir quelles sont les constantes... et ainsi de généraliser.
Puis nous verrons la mise en oeuvre de ces lois pour calculer l'orbite d'une planète, ce qui nous permettra de découvrir quels sont ces étranges paramètres orbitaux.
Ensuite, nous analyserons quelles sont les perturbations que peuvent entrainer les autres planètes. Avant de finir sur un petit aperçu de la relativité générale.
Détermination des lois de Kepler
Loi des aires, le mouvement à force centrale
Supposons avoir un point matériel central 0 de masse M et que l'on ait un point mobile P de masse m soumis à la gravité.

On pose µ=GM où G est la constante universelle de la gravitation G=6.67*10^11 m^3*kg^-1*s^-2.
On a alors l'expression du moment cinétique :
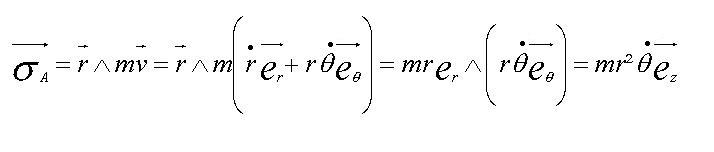
Or ce moment est constant, en effet, en le dérivant on a :
Et ainsi
Or le moment cinétique représente deux fois l'aire balayée par le rayon vecteur r pendant dt, en effet v=dr/dt... On a bien l'aire balayée pendant un certain temps qui est une constante pour les mouvements à force centrale et ainsi on a la seconde loi de Kepler.
La première loi
On a :
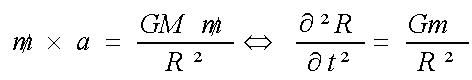
Et on pose :

Il vient alors :

Or, la cinématique nous donne :

Ce qui nous permet de savoir la valeur de l'accélération centrale, qui est en fait la seule (par hypothèse) :
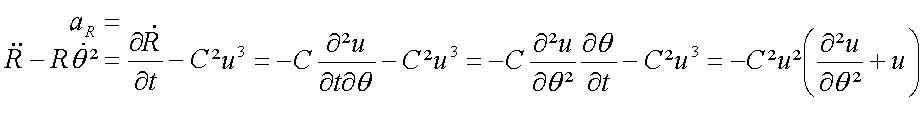
Ce qui, par le PFD (F=ma) nous donne l'équation différentielle suivante que l'on résoud :

On tombe ainsi sur l'équation d'une conique dont l'un des foyers est le soleil, et pour les planètes, on a ainsi des ellipses : c'est la première loi de Kepler. p (minuscule) désigne la paramètre de la conique, et e son excentricité.
La troisième loi
On note E l'energie mécanique du système E=Ep+Ec (énergie potentielle, énergie cinétique), le A est la constante que l'on a fait apparaitre lors de la résolution de l'équa diff ci dessus. On obtient alors l'excentricité en fonction de l'énergie. De plus, on connait la relation entre le paramètre P de la conique et son demi grand axe a, ce qui nous donne la formule.

C'est un peu embrouillé mais cela ne nécessite pas de commentaires supplémentaires, ici, P désigne la période de révolution :

Et ainsi on a la troisième loi. T²/acube=constante
L´équation de Kepler
Les trois lois de Kepler nous ont juste donné le principe du mouvement planétaire. La troisième loi nous permettrait au pire de faire un calcul de la position à partir de quelques données. Mais ce serait une intégrale, donc, pour nous, un calcul difficile et généralement approché, et pour Kepler...il ne connaissait pas le calcul différentiel. (Inventé le siècle suivant par Newton et Leibniz, la paternité ayant sucité de nombreuses polémiques...).
Il nous faut donc trouver un moyen plus agréable de calculer la position de la planète sur son orbite, ce qui est fait en résolvant l´quation de Kepler...
Les éléments orbitaux
Calculer la position d´une planète sur son orbite nécessite de définir quelle est son orbite dans tel ou tel système de coordonnées. Le système intuitif est celui des coordonnées cartésiennes : longuer,largeur,hauteur... Mais celui ci est vraiment mal adapté au calcul que l´on va faire. Le systéme polaire était adapté a la démonstration de la première loi de Kepler, mais n´est pas judicieux lorsque l´on connait l´orbite. En effet, il suffit juste de donner l´angle que fait la planète avec le périgée pour tout avoir. C´est pour cela que l´on travaille avec ce que l´on a appelé les anomalies :
E : anomalie excentrique
M : anomalie moyenne
f : anomalie vraie : angle que fait la planète entre le foyer et son périgée

Soit C le cercle apsidial, c´est à dire le cercle qui "entoure" l´ellipse. Son équation est (coordonnées cartésiennes pour l´instant) :

Et on sait que celle de l´ellipse est :

L´ellipse se retrouve donc par transformation du cercle...
 Or, on a :
Or, on a :
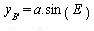
ce qui donne, par transformation, les relations entre f et E :


On a défini l´anomalie moyenne comme l´ angle que ferait une planète se déplaçant sur un cercle en mouvement uniforme, ce qui donne, en fonction du temps t et du déplacement angulaire n :
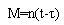

L´aire balayée par le rayon vecteur pendant 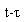 correspond à l´aire dans l´ellipse suivant APB, ce qui donne
correspond à l´aire dans l´ellipse suivant APB, ce qui donne

En effet, on a vu que

, or on a :

Ce qui donne bien :

On a aussi l´aire dans APB´ égale à

Or, on retrouve APB´ d´à partir de APB par la transformation :

(Rem : pour ceux trouvant cette évidence géométrique pas si évidente que ça, il suffit de faire l´intégrale de la fonction ellipse et de faire un changement de variable entre le y elliptique et le y circulaire, cela leur paraitra plus clair tout en étant inutile. Pour les petits malins qui s´y testeraient, il n´est pas la peine de trouver une expression de la fonction...)
Et à partir de là, on trouve :

QUI EST L´EQUATION DE KEPLER
A partir de sa résolution, on retrouve E en fonction du temps, et ainsi, d´après les formules reliant E et f, on trouve la position de la planète au temps t, tout cela dans un repère "absolu".
On peut faire de même avec la terre et, par changement de coordonnées, avoir la position relative de la terre par rapport à cette planète... Ce qui nous permet de calculer tout ( : distance, ascension droite, déclinaison...). Cela nécessite de résoudre l´équation de Kepler, ce qui ne peut se faire que de manière approchée.
Résolution de l´équation de Kepler
...En construction...


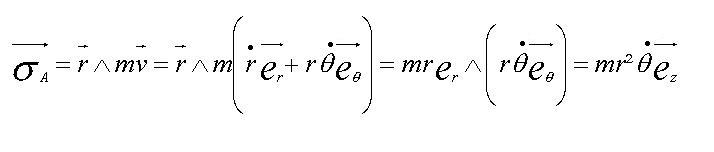
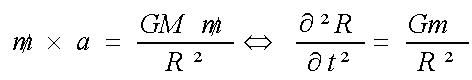



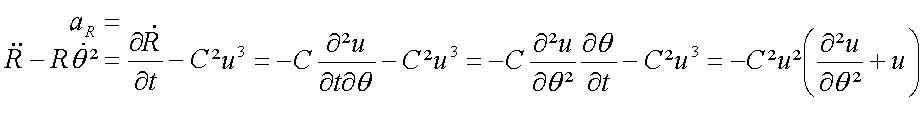






 Or, on a :
Or, on a : 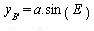


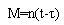

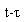 correspond à l´aire dans l´ellipse suivant APB, ce qui donne
correspond à l´aire dans l´ellipse suivant APB, ce qui donne 





