 (On ajoute qu’il connaissait le théorème de Thalès et qu’il a inventé la trigonométrie ( comme ça, par envie)). Schématisons ce qu’il savait :
(On ajoute qu’il connaissait le théorème de Thalès et qu’il a inventé la trigonométrie ( comme ça, par envie)). Schématisons ce qu’il savait :Les distances astronomiques
SOURCES : - Atlas de l’astronomie (livre de poche ; Joachim Herrmann)
- Les éclipses ( PUF ; Paul Couderc )
- Astronomie ( Larousse ; Philippe de la Cotardière)
- Méthode de l'astrophysique de L.Gouguenheim
Il ne faut pas négliger ce domaine de l’astronomie car il est la base de toute étude sérieuse : confondre un quasar au rayonnement immense avec un choc entre astéroïdes ferait perdre toute crédibilité à la science.
La recherche de ces distances se présente sous deux grands champ . D’une part, la recherche des distances dans le système solaire, qui a commencé avec les astronomes de la Grèce antique et d’autre part le calcul des distances interstellaires qui a commencé avec les premières mesures de parallaxe vers 1838 sur ‘61 Cygni’ par Bessel .
Dans le système solaire
L’histoire du calcul des distances dans le système solaire est une partie très intéressante : on voit comment, avec des moyens dérisoires, nos ancêtres nous ont légué les bases de l’astronomie.
Cette histoire est librement interprétée pour montrer la logique suivie. Pourtant, il ne faut pas y voir une avancée type " toujours plus haut ". N’oublions pas les années d’obscurantisme et de retour en arrière entre deux (re)découvertes et changement de mentalités…
Le diamètre de la terre
On pourrait s’étonner de voir que la première grande réalisation a été la mesure du rayon terrestre. Pourtant, cette elle a été la base d’un grand nombre d’études, de l’astronomie à la navigation …
Nous pouvons donc affirmer, grâce aux moyens de l’époque que la terre est ronde ( sphérique) . Et les affirmations contraires ne furent qu’obscurantisme .
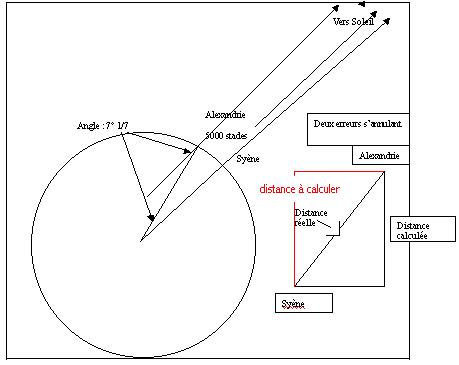
Il semble qu’Eratosthène ait été mis au courant que, lors du solstice d’été, à midi, le soleil ne donne aucune ombre au fond d’un puits à Syène ( il l’a vérifiée). Au même moment, à Alexandrie, un obélisque donne une ombre de 7°12’. Sachant que ces deux ville sont ( approximativement ) sur le même méridien, cet angle représente la différence de latitude entre les deux villes. Etant géomètre, Eratosthène a pu calculer la distance entre les deux villes : 5000 stades (800 km voir plus loin). Sachant que 7°1/7 valent 5000 stades, on en conclut que 360° valent : 5000*360/(7+1/7)= 252 000 stades. Malheureusement, il existait plusieurs sortes de stades, mais avec celui qui était le plus probablement utilisé, on trouvait environ 39 690Km ! ! ! ( ce qui est extrêmement proche de la valeur réelle ~40 000 Km).
Le calcul du rayon d’un cercle était connu depuis les Egyptiens antiques (mais pas avec le bon Pi).
On a donc :
Diamètre = 2*Pi*Rayon
ó Rayon = Diamètre/(2*Pi) soit 39690 / (2*3.14)= 6320
La terre avait donc, pour eux, 6320 km de rayon. A comparer avec nos 6370 km !!!
La précision remarquable était du au fait que l’erreur sur le méridien ( Syène n’était pas pile poil sur celui d’Alexandrie ) était corrigé par l’erreur sur la distance ( pas tout à fait 5000 stades mais plus, voir schéma). Ces erreurs avaient été vues par les compatriotes d’Eratosthène, c’est pour cela que son résultat avait été critiqué. Pourtant, il nous avait donné l’échelle de la terre ! ! !
La distance Terre Lune
Il semble que ce soit Aristaque de Samos (v -260 ) qui ait calculé le premier la distance terre lune et le diamètre de celle ci. Il avait imaginé une méthode trigonométrique et avait trouvé (donnés transférées en système métrique donc pouvant être erronées si la conversion n’est pas la bonne) 4600 km de diamètre ( au lieu de 3476) et 121 000 km au lieu de 384400km. Pour le diamètre, il semble qu’il ait observé que le diamètre de la lune était 3/8 de l’ombre portée par la terre (lors d’une éclipse) et, en supposant que le soleil était trop loin pour avoir une effet sur cette ombre, il a calculé que le diamètre de la lune était 3/8 de celui de la terre soit 3/8*12500 km ~ 4700 km.
S’il avait connu la trigonométrie avec la tangente, il aurait trouvé 500 000 km de distance [comment a-t-il fait pour trouver 121000 ? ? ?]. Aristaque avait imaginé une méthode pour savoir la distance Terre-Soleil, elle consiste à calculer l’angle Lune-Terre-Soleil lorsque la Lune est au premier quartier ( donc lorsque l’angle Terre-Lune-Soleil est droit) . En appelant D la distance terre soleil, d celle terre lune et alpha l’angle, on a :
Cos ( alpha) = d/D
D= d/ [cos (alpha)]
Je ne suis pas sûr qu’il était en mesure de faire ce calcul. Pourtant, en prenant une mesure de l’angle, il a prouvé que la distance terre soleil était bien plus grande que la distance terre lune…
Mais le premier à avoir trouvé des valeurs plus sûres et à avoir inventé une méthode de calcul précise fut Hipparque (v –190 –120) ( le même que dans Tintin " on a marché sur la Lune "). On pourrait d’ailleurs étudier tous les secteurs de l’astronomie à partir d’Hipparque : il a théorisé les mouvement des planètes à un degré incroyable (mais à partir du système géocentrique, avec les épicycles …). Il a inventé la trigonométrie avancée (: sinus, cosinus…) ainsi que la trigonométrie sphérique. Il a calculé avec précision la période de révolution de la lune, l’obliquité de l’écliptique. Il a inventé des tables de mouvement de la lune et du soleil autorisant la prédiction correcte d’éclipses. Il a fait un catalogue d’étoiles très précis en leur assignant des grandeurs en fonction de leur luminosité (6 en tout, qui donneront plus tard les magnitudes). En étudiant cette carte et le mouvement du soleil, il découvre même la précession des équinoxes, qui fait que l’étoile polaire n’a pas toujours été la même.
Il a aussi introduit en Grèce ( à partir du système Babylonien) le découpage du cercle en 360°divisibles en 60’ eux même divisibles en 60‘’.
Hipparque est arrivé à 4200 km de diamètre pour la lune et à 425 000 km de distance (un peu trop gros) et c’est Ptolémée ( +100 ;+ 180) qui en reprenant sa technique trouvera des résultats corrects : 3700 km et 376 000 km.
Valeurs actuelles ( moyennes) 3476 km de diamètre et 384 400 km .
La technique d’Hipparque :
Hipparque a été le premier à remarquer que la Lune n’avait pas un diamètre apparent fixe, il varie entre 29.4’ et 33.5’ . Sa moyenne est de 31’, c’est celle qui sera utilisée dans les calculs.
Il a utilisé les faits que :
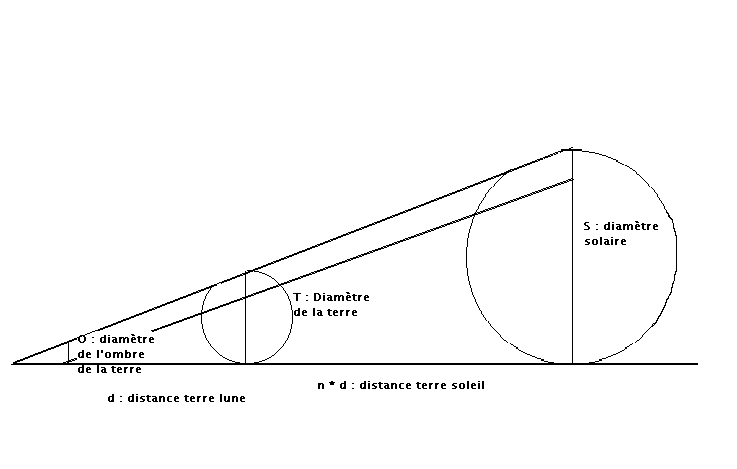
 (On ajoute qu’il connaissait le théorème de Thalès et qu’il a inventé la trigonométrie ( comme ça, par envie)). Schématisons ce qu’il savait :
(On ajoute qu’il connaissait le théorème de Thalès et qu’il a inventé la trigonométrie ( comme ça, par envie)). Schématisons ce qu’il savait :
Comme les diamètres du soleil et de la lune sont égaux, alors on a S = n * L et , d’après le théorème de Thalès on peut écrire que D ( distance terre –soleil) = n * d ( distance terre- lune) ( c’est le même n, il est bien entendu supérieur à 0).
L’observation du schéma nous montre une configuration de Thalès dans les petits triangles, cela nous donne :
(T-O)/(S-O) = d/((n+1)d)=1/(n+1)
donc (T-O)/(S-O)=1/(n+1). Sachant que O = 8/3 L ( hypothèses) et S = n*L on a :
( S-O différent de 0 ( le soleil et la lune n’ont pas le même diamètre sinon ils seraient à la même distance et il y aurait collision lors des éclipses) ainsi que n+1 différent de 0 ( voir plus haut )) .
(T-O)*(n+1) = S-O
<=> (T – 8/3*L)*(n+1) = n*L-8/3*L
<=> (n+1)*T = n*L-8/3*L+8/3*L(n+1)
<=> (n+1)*T = n*L*(8/3+1)
<=> (n+1)*T = n*L*11/3
<=> L = (n+1)/n*T*3/11
<=> L =3/11 * T * (1+1/n)
Or en supposant n très grand ( on sait que n = 400, Hipparque pouvait lui dire merci à Aristaque), on peut négliger 1/n, cela nous donne L= 3/11* T en prenant T=12700, on a un diamètre lunaire de 3500 km ce qui est une valeur correcte.
Les distances absolues et relatives
Distances relatives
Lorsque la distance Terre- Lune fut "calculée", il ne restait plus qu’à calculer celle des planètes, par rapport au soleil et à la terre, mais il fallait aussi savoir leur configuration réelle dans l’espace. Grâce à Copernic (1473-1543), le système héliocentrique, créé par Aristaque (310 – 250 avant JC ), a été réinventé et a pu se diffuser. Quelques années plus tard, Tycho Brahé (1546-1601), astronome danois, met en place un observatoire. Celui-ci lui permet, durant nombre d’années, de noter la position des planètes sur la voûte céleste. Et ses observations sont même corrigées de la réfraction atmosphérique ! ! ! Ce travail permettra à Kepler(1571-1630) de calculer ses lois.
On peut se rendre compte que la troisième loi de Kepler est T^2 :a^3= constante. Ce résultat sera prouvé bien plus tard par Newton. Cette loi toute empirique n’a pu être formulée que grâce au calcul de la période de révolution des planètes autour du soleil : T, ce qui, avec les calculs de Brahé était très facile mais aussi avec le calcul de a : distance soleil- planète. Or, Kepler fait tous ses calculs en rapport avec la terre, dont il pose sa période à 1 et son éloignement à 1 aussi. Les distances ‘a’ seront toutes en fonction de la distance terre- soleil ,ce sont donc des distances relatives, du fait qu’elles se rapportent à une autre distance, non nécessairement connue . On verra que cela facilite grandement les calculs.
Mais tout d’abord, parlons d’un sujet qui pourrait paraître totalement étranger au calcul des distances, a savoir les révolutions synodiques et sidérales. La révolution sidérale, pour une planète, est le temps entre deux passages au même point de son orbite (plus précisément entre deux longitudes héliocentriques identiques). La révolution synodique est le temps entre deux oppositions (ou conjonctions). (Rappelons qu’une opposition se produit lorsque la planète, la terre et le soleil sont alignés dans ce sens, on a une conjonction lorsque la planète, le soleil et la terre sont alignés. Pour un observateur terrestre, l’opposition se produit quand l’angle entre le soleil et la planète est de 180°, donc, c’est la période la plus favorable pour les observations).
Prenons deux planètes, comment calculer la révolution sidérale sachant la révolution synodique et inversement ? ? ? Soit t1 et t2 (t1temps le plus court) leurs temps de révolution sidérale(en jour par exemple) et prenons les angles en degré ; leur mouvement angulaire (journalier) sera donc 360:t1 et 360 :t2 leur différence de mouvement angulaire sera donc 360 :t1-360 :t2= 360(1:t1-1 :t2) donc le temps mis pour que les planètes se retrouvent dans les mêmes positions l’une par rapport à l’autre, soit la révolution synodique sera de 360 par le précédent rapport donc 1 : (1:t1-1:t2) et donc 1:Rsyn= (1:t1-1:t2) …

Les premières distances relatives des planètes furent trouvées dès Copernic, ce fut celle des planètes inférieures, Mercure et Vénus. En effet, on s’était aperçu que Vénus s’éloignait du soleil (élongation) au maximum de 46° (entre 45 et 47) et Mercure de 21.5° (entre 16 et 27). On prend ici les valeurs moyennes. En faisant un schéma, on comprend tout de suite pourquoi, à ce moment là, l’angle Terre- planète inférieure- Soleil est égal à 90°. La trigonométrie nous montre tout de suite qu’en prenant pour unité la distance terre- soleil (UA), le sinus de l’élongation maximale était égal à la distance terre planète en unités astronomiques (UA). Par exemple, pour Vénus, sin(46°)=0.72, donc Vénus est en moyenne à 0.72 (0.723) unités astronomiques du soleil, Mercure est elle à 0.37 UA (0.387).

Lorsque l’on cherche à calculer la distance des planètes plus éloignées de la terre telles les planètes extérieures, on se heurte à un autre problème : lorsqu’une telle configuration est faite, l’élongation de la planète est de 90°, on ne peut donc rien calculer comme précédemment il faut calculer l’angle Terre- soleil- Planète, comme on n’observe pas sur le soleil, Kepler a trouvé un truc. Il suffit de prendre comme hypothèse que la planète a un mouvement angulaire constant, ainsi que la terre. Les observations prouvent que cette approximation est légitime.
Comment faire ?
On observe une planète extérieure, comme Mars, et on calcule son temps de révolution sidérale. On calcule le temps entre son passage à l’opposition, c’est à dire quand l’angle Mars-Terre-Soleil est plat, et son passage en quadrature, quand l’angle est droit. Comme on a supposé que les planètes allaient à des vitesses angulaires constantes et à des distances constantes du soleil, on peut facilement calculer les angles Alpha et Béta :
Si T est le temps mesuré, t1 le temps de révolution de la Terre et t2 celui de Mars (exprimés dans les mêmes unités) on a :
Alpha = T/t1*360°, Béta=T/t2*360°.
L’angle Alpha moins Béta, que l’on note A, nous permet de tout calculer. En effet, A est l’angle Terre-Soleil-Mars quand l’angle Soleil-Terre-Mars est droit. L’inverse du cosinus de A ( : 1/cos(A) ) est donc la valeur de la distance Soleil – Mars en unités astronomiques.
En factorisant, on a A=360*T*(1/t1-1/t2) en reprenant l’expression de la période de révolution synodique on a :
A=T/Tsyn*360
Exemples :
Jupiter était à l’opposition le 1/1/2002 et en quadrature le 27/3/2002 soit un T de 87 jours (en tenant compte de quelques petites imprécisions).
Comme Tsyn=398 on a A=78,69° donc 1/cos(A)=5,1 SOIT 5,1 UA ce qui est proche des 5,2 UA des livres.
Mars était à opposition le 13/6/2001 et en quadrature le 14/10/2001 soit un T de 123 jours.
De plus, Tsyn=780 jours donc :
A=56,77° et 1/cos(A)=1,82 soit 1,82 UA! ! !
Sachant que le demi grand axe mesure 1,524UA, on est étonné.
Mais c’est là le plus intéressant, les calculs sur Mars avec l’approximation précédente contredisaient les expériences, le modèle était à revoir. A partir de ce type de calculs, Kepler a trouvé ses trois lois, qui serviront de base à la dynamique et donneront à Newton l’idée d’une force de gravitation proportionnelle à 1/r².
D´ailleurs, Kepler a aussi utilisé une autre technique qui lui a permis de savoir quelle était la vraie nature de l´orbite de Mars : sachant la période de révolution de Mars, il peut l´observer plusieurs fois ( à quelques années d´intervalle) alors qu´elle est à la même place. Or,la terre n´est pas à la même place. Donc on peut trianguler la position de Mars et ainsi avoir la forme de son orbite... (Il est possible de calculer la distance absolue par cette méthode mais le résultats sont imprécis).
Distances absolues
Au début du 17ème siècle, on connaissait donc les distances relatives des planètes correctement et on pouvait faire des calculs précis… Il suffisait de mesurer de manière absolue une distance et on les avait toutes. Mais cette mesure de l’unité astronomique était la plus dure, en effet, aucune astuce géométrique ne pouvait permettre aux astronomes de la calculer en restant dans le confort de leurs observatoires. Il fallait faire des expéditions à l’autre bout de la planète pour mesurer la " parallaxe horizontale ".
La parallaxe horizontale est l’angle formé par la droite joignant l’astre au centre de la terre et l’autre joignant l’astre et un point de la surface de la Terre où il se couche, soit en notant (grand) PI cet angle :

On comprend mieux pourquoi des dizaines d’expéditions se sont montées pour mesurer l’UA.
L’unité astronomique
Grace à Fizeau, on a pu connaitre en 1849 la vitesse de la lumière indépendemment de toute observation astronomique. Et ainsi on peut mesurer les distances des planètes ( et ainsi en déduire l´UA) par mesures radar (plusieures ont été faites dans les années 60 sur Vénus) . Par effet Doppler, on peut aussi calculer la vitesse de la terre et ainsi calculer son rayon(moyen) et donc l´UA (Adams 1940).
Distances stellaires
Parallaxe : on utilise la même relation que pour les planètes mais au lieu de se positionner sur 2 points du globe, on effectue les mesures sur 2 points différents de l'orbite, pour une meilleure précision, on choisit le plus grand écartement possible et ainsi on prend des mesures à 6 mois d'intervalle. La première mesure date de 1838 : Bessel calcula la parallaxe de 61 Cygni : 0,3". Par la même méthode, on a trouvé que l'étoile la plus proche du soleil ( soleil non compris bien sûr ) est Proxima du centaure qui a une parallaxe de 0,765". On prend pour unité de distance le parsec (pc)( : la distance pour une parallaxe d'1") qui vaut 3,09*10^16m ou 3,26 anné lumière. Ainsi, 61Cygni est à 3,41pc et Proxima à 1,31pc.
Parallaxe séculaire : au lieu de se baser sur le mouvemet de la terre, on utilise le mouvement propre du soleil dans la galaxie. Mais comme les étoiles bougent de manière non négligeable durant les temps nécessaires, il faut utiliser certaines astuces pour avoir des calculs corrects.Elle s'applique à des ensembles d'étoiles. Par exemple, si certains types d'étoiles sont trop éloignés pour que l'on puisse utiliser la parallaxe habituelle on en prend un échantillon (sur tout le ciel) dont on peut ainsi supposer la vitesse moyenne nulle. On peut calcule la valeur moyenne des parallaxes séculaires de ce groupe qui nous donne la valeur moyenne de la distance. On peut calculer les distance de chaque étoile par des considérations de luminosité.
Parallaxe statistique : comme la dernière méthode, elle s´applique sur un groupe d'étoile.Par effet Doppler, on peut calculer la vitesse radiale des étoiles, statistiquement, on peut à partir de celle-ci calculer la vitesse moyenne absolue! des étoiles. A partir de leur vitesse moyenne et radiale, on peut calculer la vitesse transversale. Couplée au déplacement apparent, celle-ci permet de calculer la distance. On peut dire que cette méthode est une parallaxe "à l'envers" puisque les mesures des points différents sont non citués sur la terre mais sur l´étoile. Cette méthode est précise pour des groupes d´étoiles ayant une vitesse relative assez rapide.
Courant d´étoiles : Variante de la dernière méthode, avec un calcul de vitesse différent : les étoiles des amas ont des mouvement quasiment parallèles, or, en pratique, elles semblent se diriger vers un point, a partir de celui-ci, on arrive à savoir les composante des vitesses...
Eclat apparent : si l´on connait la luminosité L, c´est à dire la puissance totale rayonnée par l'étoile, on peut calculer sa distance à partir de la puissance reçue par un récepteur sur terre : l´éclat apparent.
Magnitude apparente et absolue : C'est la même méthode sauf que l'on remplace la luminosité par la magnitude absolue et l'éclat apparent par la magnitude apparente.
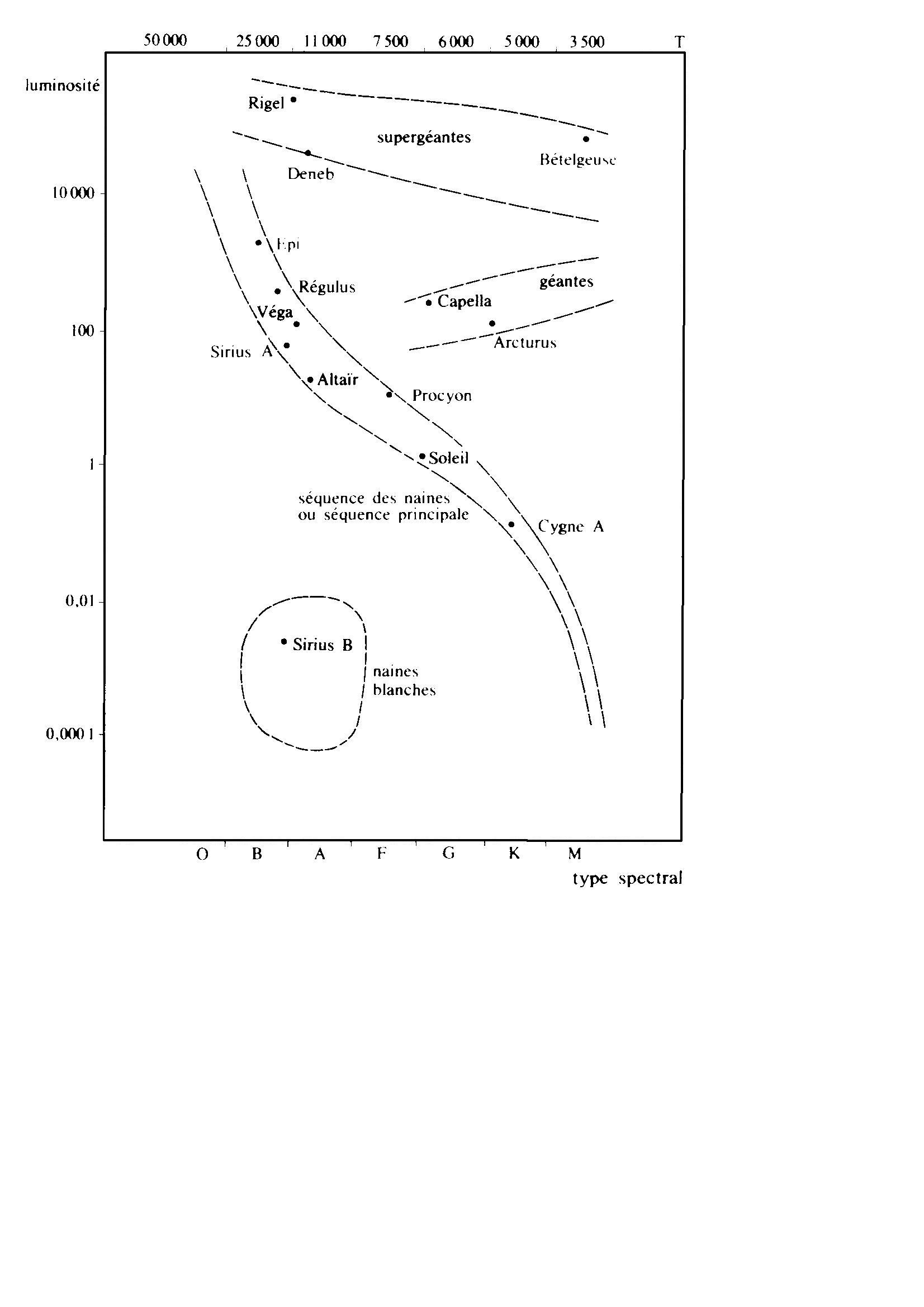
Diagramme Hertzsprung-Russell : en 1911 et 1913 les astrophysicens Hertzsprung et Russell ont créé un diagramme montrantune relation entre la luminositér et la température des étoiles. Or, la couleur nous donne la température (qui nous donné le type spectral). Donc on peut très facilement trouver les donnés pour calculer les luminosités ou magnitudes absolue ( à partir d'étalons) et ainsi il est facile de calculer la distance des étoiles
Sur le schéma, on peut voir comment se placent les étoiles, le plus intéressant est la séquence principale qui est aussi "là" où les étoiles passent la majorité de leur existence. En effet, ce schéma représente d'une certaine manière l'évolution des étoiles mais c´est un autre problème...