Les calculs de trigonométrie sphérique

Avant propos :

Ce document a pour but de démontrer les calculs trigonométriques très utilisés en astronomie.
Il doit normalement être du niveau 1ère S ( et lycée tout court car j'expliquerais prochainement les principaux axiomes : la configuration des sinus et cosinus ainsi que le produit scalaire).

La trigonométrie est l'étude des relations entre les angles d'un triangle, son but est de fournir des équations simples pour trouver les donnés qui nous manquent. La trigonométrie peut ainsi permettre de connaître la distance d'une étoile, de calculer la phase d'une planète ou de la lune... Pourtant, pour changer de coordonnées célestes, la trigonométrie simple n'est plus utilisable, il faut travailler dans le triangle sphérique. Mais qu'est-ce qu'un triangle sphérique ???
Le principe est simple. Un triangle sphérique est la plus petite portion d'une sphère limitée par 3 grands cercles (cercles centrés en O ( centre de la sphère) et de rayons celui de la sphère); cette définition étant un peu barbare, on simplifiera les choses en dessinant un triangle sur une feuille que l'on posera sur quelque chose de sphérique (ballon ...). Les lignes droites étant transformées en courbes (dont le prolongement sera un cercle de même rayon que la sphère) .

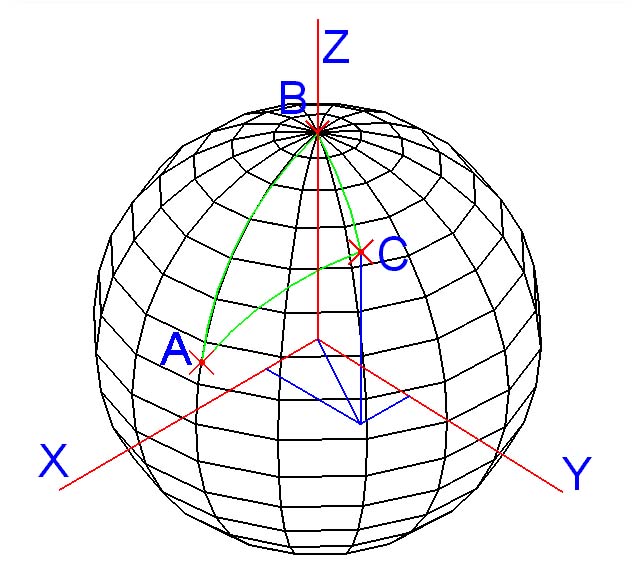
Les trois points sur la sphère délimitent le triangle sphérique.
L'image ci-dessus présente la sphère dans sa configuration initiale : B est sur un pôle de l'axe z , A est un point d'intersection de la sphère avec le plan passant par les axes z et x.
Par définition, les angles du triangle sont notés A,B et C donc l´angle ABC sera noté B, BAC sera noté A... . Le coté opposé à un angle a la même dénomination que celui-ci mais en minuscule. Le côté BC sera ainsi nommé a et BA sera nommé c. Comme on est sur une sphère de rayon 1, on peut confondre un coté et un angle, ainsi a=BOC ...Attention, B est différent de b et ainsi de suite...
Pour faciliter les calculs, nous parlerons en radians (PI rad=180°) et on prendra une sphère de rayon 1.

Notre but est de calculer les coordonnées x,y,z de C situé sur un point quelconque de la sphère. On les recalculera avec un repère différent, et après avoir rendu les données compatibles (changement de repère), on pourra les écrire comme équivalentes. Ces relations seront celles de trigonométrie sphérique.

Vous constaterez que chaque figure est représentée deux fois. Grâce à ce petit artifice, nous pourrons nous représenter une sphère. En effet, cela nous permet d'avoir une coordonnée en z et en y sur le 1er schéma et le 2ème, avec une coordonnée déjà connue, nous permettra de connaître x. Ces projections ne changeront pas la valeur des angles A,B,C (ou de manière négligeable, (ce litige est à démontrer, un exercice pour vous; solution en annexe)).

1: COORDONEES DE C

fig1a

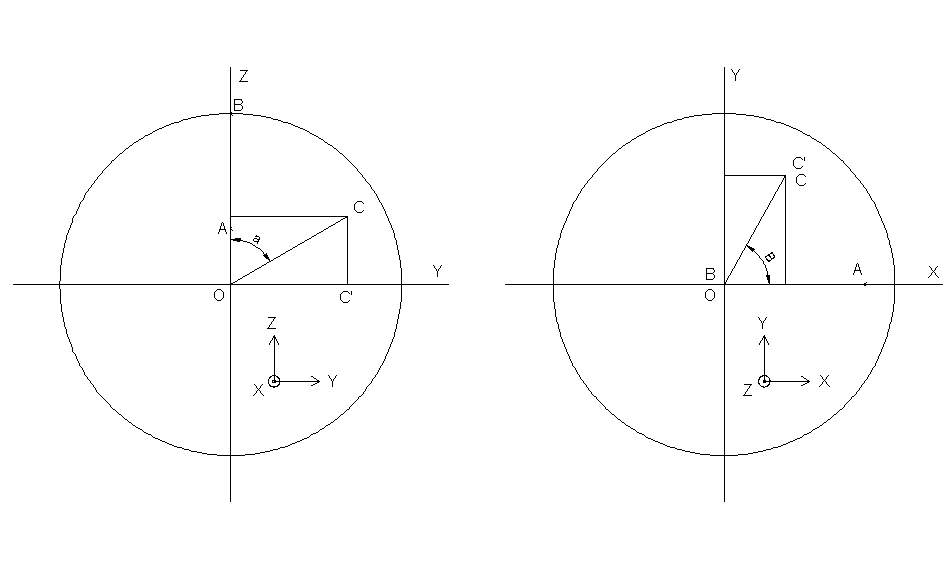fig1b

La projection de C sur le plan y x est nommée C'. Pour trouver les coordonées y et x il faut trouver la valeur OC' . Après, cela se rapporte à un calcul de trigonométrie normale (fig 1b).
Par définition, l'angle BOC est a. La fig1a nous montre un triangle tout ce qui a de plus simple. ( La projection fig1a n´est pas tout a fait exacte, en fait,ce n´est pas le plan xOy mais le plan COB, cela n´influe en rien sur les calculs ). On calcule grâce à lui z et OC':

z= sin(C'OC) = sin(PI/2-a)=cos a

OC'=cos(C'OC)= cos(PI/2-a)=sin a

Rappel : sinus = côté opposé/ hypoténuse; cosinus = côté adjacent/hypoténuse
donc : sinus*hypoténuse=côté opposé; cosinus*hypoténuse= côté adjacent.

Pourquoi utilise-t-on l´angle B dans la projection fig1b au lieu de b? Il faut se rendre compte que notre triangle est sphérique, soit en 3D et on veut calculer ABC´. Si on utilisait b, comme A et C ne sont pas obligatoirement dans le plan xOy, on peut avoir un angle beaucoup plus grand que celui de la projection...Il nous faut donc un angle qui soit correct par cette projection, c´est B ( voir ci-dessous).

Pour trouver les coordonnées de C, on n´a plus qu´à calculer les coordonnées de C´ dans le plan xOy, sachant que la longueur de l´hypothénuse est sin a, on en déduit les coordonnées du point C :

x =OC'* cos(ABC)= sin a * cos B ;

y =OC'* sin(ABC)= sin a*sin B ;

z = cos a ;

Après, on fait tourner la sphère autour de l'axe y de manière à ce que A remplace B. Pour les puristes, on choisit un nouveau repère orthonormé direct centré sur O, avec des vecteurs unitaires de même norme que le précédent, dont l´axe des ordonnées est aussi le même et dont le nouvel axe des z est OA. Ce qui nous donne :

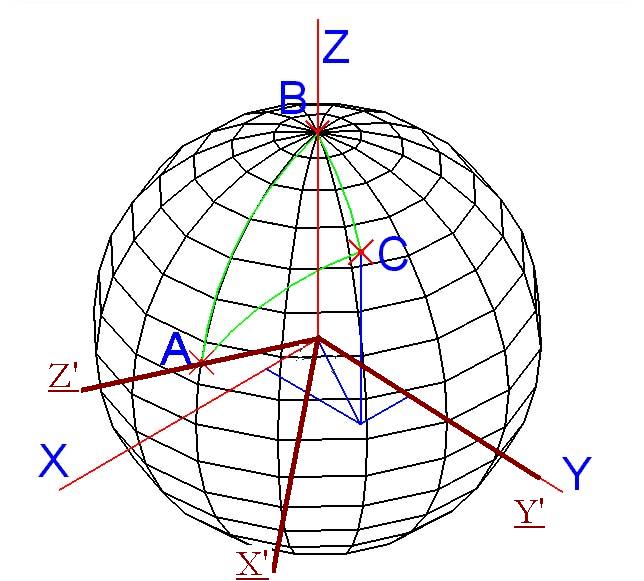Nous avons notre nouveau repère orthonormé : (O,X',Y',Z').

Fig2a

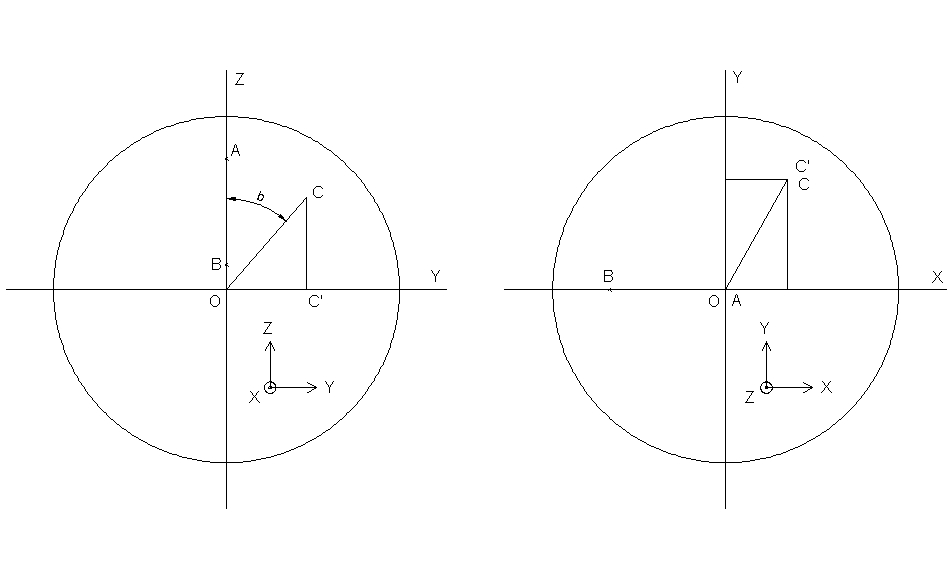fig2b

On remarque que c´est le même type de projection qu´on a utilisé précédemment, avec la même erreur sur la fig 2a : on a projeté sur le plan ZOC et non ZOY . On aura donc :

z' =sin(C'OC)=sin(Pi/2-b)= cos b;

OC' =cos(C'OC)=cos(Pi/2-b)= sin b;

Par contre, du fait que le A dans 1b n'est pas du même côté que B dans 2b, on ne parlera pas de cos ou sin A mais de cos ou sin PI-A. Or, suivant la configuration des sinus et cosinus, cos(PI-A)= -cos A, sin PI-A=sin A. Donc les relations seront :

x'=OC' * cos(XAC)= sin b*cos(PI-A)=-sin b*cos A;

y'= OC' * sin(XAC)=sin b *sin (PI-A)=sin b*sin A;

z'=cos b;

2 : LES RELATIONS DE TRIGONOMETRIE SPHERIQUE

On utilise les relations de changements de repère ( voir annexe) qui sont :

x= x'*cos c +z'*sin c

y= y'

z= z'*cos c-x'*sin c

Remarque : cette formule a été déduite de l´annexe en remplaçant y(annexe) par x et x(annexe) par z en effet, pour que les formules de l´annexe s´appliquent, il faut être dans une base (x,y,z)directe.

On laisse les formules 1 inchangées:

x= sin a*cos B;

y= sin a*sin B;

z= cos a ;

Et on change les formules 2 :

x= cos b*sin c -sin b* cos c *cos A ;

y= sin b * sin A;

z= cos b*cos c+sin b*sin c*cos A;

On a donc deux formules de coordonnées de C dans le même repère, elles sont égales, il suffit de remplacer x et on trouve :

Les formules de trigonométrie sphérique :

sin a*cos B= cos b*sin c -sin b* cos c *cos A ;

sin a*sin B= sin b * sin A;

cos a = cos b*cos c+sin b*sin c*cos A ;

A noter : la seconde est peu utilisée.

 

 

 

Annexe : formules de changement de repère :

Ceci est un cours que l'on voit en exemple en 1ère S. Mais avec un cercle !
Pourtant, c'est celui que nous allons utiliser. En effet, nous avons fait tourner la sphère autour de l'axe y . Donc, en faisant une projection de manière à ne voir que les x et les z, nous aurons notre cercle!!!

Cela nous donne :

 

On a C,B et B' qui sont sur le cercle . (OB) est perpendiculaire à (OC).

Nous avons dans ce schéma 2 systèmes de cordonnées :

1) le système de cordonnées initial, centré sur O, d'abscisse l'axe OB et d’ordonnée l'axe OC .

2) le système de cordonnées finales, centré sur O, d'abscisse l'axe OX et d’ordonnée l'axe OZ ( on notera OY par la suite).

Notre but est de trouver les coordonnées de B' à partir des coordonnées de B et de l'angle alpha , BOB' il est direct ( sens inverse des aiguilles d’une montre) sur le schéma, s’il n’était pas direct, alpha serait négatif, les formules restant valables.

On commence par calculer les cordonnées de B' dans le système 1 que l'on notera (X,Y) ; on notera [OB'] la longueur entre O et B' :

X = [OB'] *cos alpha ;

Y = [OB'] * sin alpha ;

Un vecteur est une flèche donnant une norme (longueur), un sens et une direction. Si on multiplie un vecteur par un entier, on multiplie sa norme par cet entier et on aura un autre vecteur de même sens, même direction et avec la nouvelle norme, plus intuitivement, c’est comme si on étirait le vecteur . On dit que les coordonnées d'un point sont la projection de celui-ci sur le vecteur I ( la notation du vecteur en gras est souvent utilisée dans les livres ).

Par exemple, si on prend A(x,y), quelconque on peut dire que les cordonnées de A sont :

A= x * I + y * J;

(Remarque, dans la base (O,I,J).

Prenons la base (O,I,J) avec I vecteur unitaire de direction Ox , J vecteur unitaire de direction Oy.

On aura donc pour OB' :

OB’= [OB'] * cos alpha * OB + [OB']* sin alpha * OC; Attention de ne pas confondre OB’ et OB.

Mais, par définition, [OC] = [OB] =[OB'] , on peut donc écrire :

OB' = cos alpha * OB + sin alpha * OC

Or, OB = x * I + y * J ; et, comme OC lui est perpendiculaire OC = -y * I + x * J . ( en effet pour A(x,y) et B(x',y') perpendiculaires. On a, par définition, x*x' + y'*y = 0).

On aura donc :

OB' = x*cos alpha*I + y * cos alpha*J - y * sin alpha* I +x * sin alpha *J

OB' = (x*cos alpha- y*sin alpha) I + ( y*cos alpha + x*sin alpha) J

Ce qui est équivalent à :

X(OB')= x*cos alpha- y*sin alpha

Y(OB')= y*cos alpha+ x*sin alpha

Donc les changements de cordonnées se feront ainsi, le nouveau x, NX sera l'équivalent de x*cos alpha - y sin alpha et le nouveau y, NY sera l'équivalent de y*cos alpha+ x*sin alpha CQFD .

 

Pour ceux qui sont allergiques aux vecteurs voilà une autre idée de démo proposée par Maurice THIEBAUT :

 

Les formules qui permettent de trouver les coordonnées après un changement d'axe.

Rotation autour de l'axe Y d'un angle C.

 

 

 

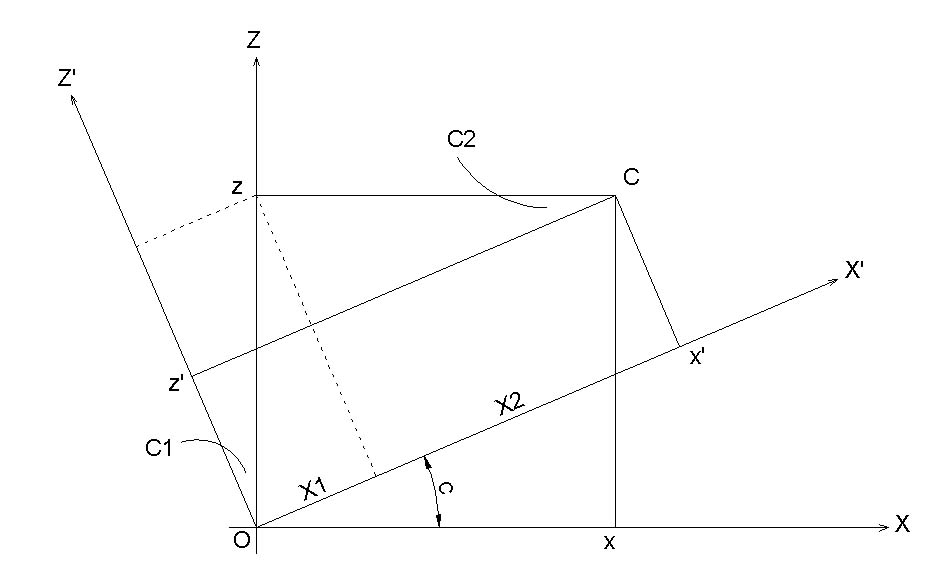
Trouver la valeur de x'

x' = X1 + X2

sin C1 = X1 / Z X1 = Z sin C

cos C2 = X2 / X X2 = X cos C

x' = x cos C + z sin C

 

 

 

 

Trouver la valeur de z'

z' = z1 – Δz

cos C1 = z1 / z z1 = z cos C

sin C2 = Δz / x Δz = x sin C

z' = z cos C – x sin C

On trouve donc bien le même résultat…

 

Mais comment faire les changements inverses ?

Il suffit de remplacer l’angle C par –C et on trouve x’= x cos C – z sin C ; z’ = z cos C + x sin C. CQFD.