A) les changements de coordonées :
Nous avons déja vu que les systèmes de
coordonnées astronomique utilisent la sphère céleste. Mais, à
l'exception des coordonnées horaires et équatoriales, elles ont
toute un zénith différent... Il faut donc trouver un moyen de
passer des unes aux autres !
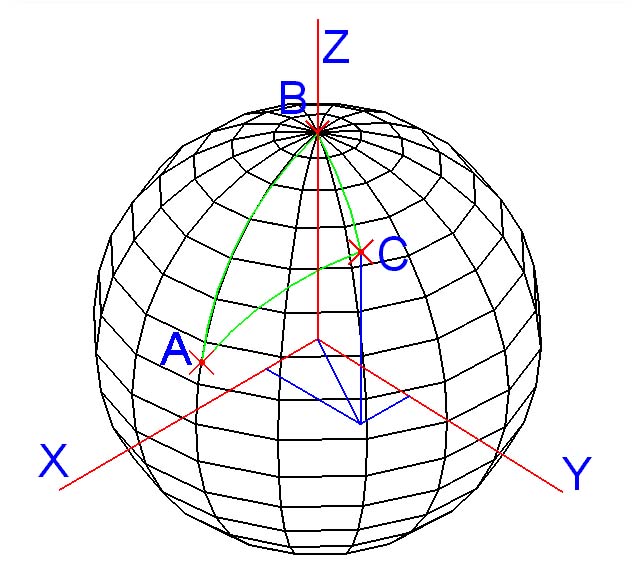
Réétudions por cela notre triangle sphérique :

Et prenons, tout bêtement, le point B
comme système de coordonnées 1 et le point A comme second système.
Après cela, il faut trouver la distance (grâce aux relations)de
l'angle...
Exemple :
Passage des coordonnées horizontales aux coordonées horaires
Prenons a, l'azimuth et h la hauteur. PSI est la latitude du lieu. Delta est la déclinaison et H l'angle horaire (à qui, pour retrouver alpha, l'ascension droite, il suffit de soustraire le temp sidéral local !( voir temps.html)
 Un petit dessin ?
Un petit dessin ?
Reprenons nos relations ( nous parlons toujours en radians a a été remplacé en an pour ne pas le confondre avec l'azimuth).
sin an*cos B= cos b*sin c -sin b* cos c *cos A ;
sin an*sin B= sin b * sin A;
cos an = cos b*cos c+sin b*sin c*cos A ;
n'oublions pas que :
sin( PI/2 - s) = cos s // ; //cos (PI/2-s) = sin s
sin (PI-s) = sin s // ; // cos(PI-s)= -cos s
et mettons les avec les nouvelles notations :
La relation 1 devient :
sin (PI/2-delta)*cos H = cos(PI/2-h) * sin (PI/2-psi) - sin(PI/2-h) * cos( PI/2-psi) * cos (PI-a)
==>> cos(delta)*cos H = sin h * cos psi +cos h * sin psi * cos a
==>>cos H = (sin h * cos psi + cos h * sin psi cos a )/ cos delta
La relation 2 devient :
sin(PI/2- delta) * sin H = sin(PI/2-h)*sin(PI-a)
==>> cos delta * sin H = cos h * sin a
==>> sin H = (cos h * sin a)/ cos delta
Et la relation 3 devient :
cos(PI/2-delta) = cos(PI/2-h) * cos (PI/2-psi)+sin(PI/2-h) * sin(PI/2-psi) * cos(PI-a)
==>> sin delta = sin h * sin psi -cos h *cos psi * cos a
On a donc delta ( en faisant ASIN). Car arcsinus (sin^-1 sur les calculettes) nous renvoit un nombre entre +PI/2 et -PI/2, pile-poile dans le domaine de définition de delta .( +PI/2 rad = 90 ° et -PI/2 rad = -90°)
ACOS nous renvoit un nombre entre 0 et
PI (0 rad = 0° et PI rad = 180°). Il y a un problème, soit on
doit avoir, en plus, des résultats entre Pi et 2 PI, soit entre
-PI et 0 !!!.
Nous avons une autre soltuion : puisque nous connaissons SIN H et
COS H, on peut dire que ASIN H nous renvoit un résultat sur le
signe et ACOS H un résultat sur la valeur !
Passage des coordonnées horaires aux coordonées horizontales
On effectue pour cela un
changement de repère dans le triangle Z,P,A. Cela nous change
les inconnues.
On écrit après ceci
=>sin h= sin psi * sin delta +cos psi * cos delta cos H
=>sin a = (cos delta * sin H)/(cos h)
=> cos a = (sin psi*cos delta*cos H - cos psi* sin delta)/(cos h)
Les autres changements de coordonées se font de manière similaire à l'exception du passage des coordonées horaires aux coordonées équatoriales ( qui se font par un chagement des valeurs de l'angle horaire voir les coordonnées ).
B) l'équation du temps :
Lorsque nous regardons un cadran solaire, on peut être étonné de voir qu'il ne nous offre pas la bonne heure TU
(Et au vu de la différence, ce ne peut être l´oeuvre de l´ET).Qu´en est-il donc???
L´ ascension droite (AD) du soleil (sa longitude, pour simplifier) augment quotidiennement du fait du déplacement de la terre autour de lui.
Malheureusement, cette AD n´augmente pas régulièrement car :
- Le soleil ne se(mble) déplace pas sur l´equateur céleste mais sur l´écliptique.
-Sa vitesse (apparente) n´est pas constante, la terre se rapprochant et s´éloignant de lui.
C´est pour contrer ces erreurs que le TU à été inventé.
Le temps solaire vrai représente l´angle horaire du soleil, le TU celui d'un soleil fictif se déplacant sur l´équateur céleste à vitesse constante.
L´quation du temps (E) est la différence entre l´ngle horaire du soleil apparent et celui du soleil fictif.
On peut donc écrire :
E = L - alpha ; L étant la longitude du soleil fictif, or L est utilisé fréquement dans le calcul de la position du soleil.
On a ainsi : C= lambda - L, lambda étant la longitude du soleil (par rapport à l´écliptique) et C l´équation du centre du soleil. Donc :
E=L-alpha=(lambda-alpha)-C
lambda , alpha et C se calculant facilement.(pour une machine).
Il suffit juste de convertir E en minute, en multipliant le résultat par 4, ou en heures, en le divisant par 15.
C) calcul des heures de lever et coucher des astres :
Calculer l'heure du lever ou du coucher d'un astre, c'est calculer à quelle heure cet astre a une hauteur de 0°.
Or, on a calculé que :
sin h = sin psi * sin delta +cos psi * cos delta *cos H.
On a donc :
=> cos H = ( sin h-sin psi * sin delta ) / (cos psi * cos delta)
En traduisant H en temps, nous avons deux valeurs possibles( + ou - ACOS(H) ) pour cet angle horaire : une entre 0 et 12 h, l'autre entre 12 et 24 h. Cela nous permet de choisir entre le calcul du lever et celui du coucher de l'astre .
Nous déduisons donc l'heure sidérale ( S)du lever le l'astre : S = H + alpha. (alpha que l'on trouve dans les éphémérides).
On calcule ensuite combien d'heures sidérales il s'est écoulé depuis 0H TU jusqu'à l'heure sidérale de Greenwich du lever de l'astre ( si vous n'habitez pas sur le méridien SG = S - L (L latitude du lieu exprimé en temps faites ensuite SG0-SG).
Voilà, vous avez l'heure du lever de l'astre ( faites un arrondi de cette valeur en raison des incertitudes sur l'heure de votre montre , l'incertitude de votre location, de la réfraction atmosphérique...).

fg
fg
fg